Introducing OnlineJudge.app

Now problem authors can put their problem-set on their blog and use OnlineJudge.app to judge its submissions.

Simple Sum

Given two integers, output their sum.

Migrating to Blogger

Believe it or not, this site is hosted on Blogger!

I just realized how customizable Blogger theme is. It allows you to edit the entire layout (using xml that allows you to "program" the html and css). I managed to keep the iconic header of my site, and use an existing theme for the contents and navigations.

Back in year 2000, I wrote PHP script for my site connecting to MySQL database to store the posts and comments. I was 18 years younger back then and had plenty of time to code. The problem is, sometimes I will need to migrate the site to another server and I don't have the time. I was thinking to convert it to a static site so that server migration will be as simple as copy-pasting (no database setup needed), but still converting the layout is a painful experience.. Do I have to copy paste the header and footer to all the pages? Then there is this idea of using Angular to create a static bundle like how the angular.io site is built for the tutorials and docs, and host the comments in Firebase, but as I said, I don't have the time to build it. There has to be a better way...

I decided to take a chance of migrating my site to Blogger (it has been around for almost 20 years now and there's no sign of being shutdown). The offered functionalities are basic, but I did try including a <script> tag and it runs. I think I can do a lot fancy stuffs with it. Nowadays, static sites (that can run Javascript) can pretty much do anything by calling API to other servers.

I will gradually migrate my old contents to this site as I have the time ...

Kawal Pemilu 2014

How does Kawal Pemilu work? See my answer at Quora and the system design document.

Nasional

Nasional

Color Legend

Prabowo / Hatta

Jokowi / JK

---

The data source for number of votes is taken from KawalPemilu.org and imported into Google Fusion Tables.

The data source for the administrative boundary map is taken from PemiluAPI.

I manually reconcile the IDs from shapefiles in the PemiluAPI with the IDs from KawalPemilu.org.

The datasets for each level of administration (for more details, click File -> About this table):

• Province
• Regency
• District
• Village (only Surakarta is available)

ACM ICPC Jakarta 2013 - Problem J - Alien Abduction Again

Last year contestants (or contestants who practiced with last year ICPC Jakarta 2012 problemset) should immediately know, only by looking at the problem title, that this problem is related to last year Problem H - Alien Abduction. Also, they should have guessed that this problem is either as hard, or harder than last year :D.

It took me several weeks to come up with this problem (and the solution). My criterion for the problem are:

• The problem must be hard. This is necessary to avoid the embarrasement (to the problem-setters) that some teams sweept clean all the problems in 3 hours >.< (yes I'm talking about you, +1 ironwood branch).
• The problem must be a rare problem. That is, I want it to be the decider problem to separate the teams at the top. I do not want to pick the problem from the Competitive Programming Book Chapter 9 - Rare Topics, because it would be too obvious :P.
• The problem must have a secret message. Well... the secret message is meaningless for any contestants (i.e., the message will not help anyone to gain better insight in solving the problem). Instead, the secret message was intended for one of the special guests in the closing ceremony :).

Given the criterion above, how should I write the problem? I search for inspiration by reading blogs, TopCoder forum posts, etc. After two weeks I decided to write a BIT (Binary Indexed Tree) with range update. I always surprised by BIT that it can be used differently than its original design (prefix sums). For example, BIT can be used to compute range minimum query, and range updates too (see Petr Mitrichev blog as well as the links in the comments section).

Here is the problem statement, you can try submit your solution below.

In short, the problem statement is like this (Click here to see the full problem statement):

Given lines/curves segments as a set of functions f_p(x) = ax³ + bx² + cx + d, each on a range [x1_p, x2_p], what is the total sum of the y-values of the points (generated by the functions) with integral x-values in range [x1, x2] ?

Naively, this problem can be easily solved using (Lazy) Segment Tree + coordinate compression. I do not want this solution to pass (remember that I want to create a BIT range update problem). Coordinate compression is a trick to make the input range smaller by pre-reading all input data and then make it dense. This will help the Segment Tree solution that it only needs to allocate 100K instead of 1M tuples. Luckily, there is a trick to make coordinate compression to fail: make it as an interactive problem. However, ICPC style usually do not involve interactive problems, so I have to uglify the input that the next input depends on the previous output of the program (i.e., to simulate an interactive problem). This is the reason that "the space distortion" was introduced every time the transporter is used. With this, coordinate compression will no longer work, but I agree that this made the problem harder to read. In fact from the survey, almost half of the teams voted problem J as the least liked problem :(. I guess that's the price I have to pay.

What about the (Lazy) Segment Tree? How to make it fail to work? I know that normally, in programming contests, two solutions with the same complexity should both get Accepted. But, this problem is an exception. I made it clear in the problem statement that your solution must be very-very efficient (otherwise the device will be too late to disrupt the transport operation by the alien ship). So, constant factor matters in this problem. I was hoping that the contestants realize that when reading the problem statement.

If you are familiar with Segment Tree, you should have an insight how slow it can be. Thus you should pick solutions with lower constant factor if any (e.g., Binary Indexed Tree). The Segment Tree solutions run in 5+ seconds while the BIT solutions run in less than 2 seconds. Moreover, the memory consumption for Segment Tree will exceed 64 MB. If you recall, in the briefing, Suhendry mentioned that all of the judges solutions use less than 32 MB. That should give you another hint that Segment Tree is not the way to go.

Unfortunately, due to PC2 inaccuracy in measuring the time limit, some teams got lucky to get it accepted with Segment Tree (albeit, they need to insanely optimize their code to get it run in 5 seconds). We set the time limit for this problem to be 4 seconds in the PC2, but somehow PC2 still accepts solutions with 5 seconds runtime! I didn't re-adjust the time limit to 3 seconds during the contest and decided to let it be (otherwise I will be cursed by the accepted teams :P).

No team solved this problem using BIT range updates. It is not easy to convert a (Lazy) Segment Tree into BIT range updates. It probably deserve a problem on its own. To give an example, consider the simplest case where f(x) = d. That is, the values for a, b, and c are all zero. In this case, the problem is equal to a very simple BIT range update. Here is a nice post on how to simulate a (Lazy) Segment Tree using two BITs. We can generalize this for the other powers (a, b, and c) and we will need five BITs. The runtime for this approach is less than 2 seconds and it consumes only ~20MB memory. This problem also requires the knowledge of mod-inverse. That is, you will need to do division with modulo somewhere in the calculation.

Well, the first two criterion have been fulfilled. The last criteria is the secret message. I hid the message in plain sight. No other judge (even the chief of judge) was aware that there was a secret message. But no worries, the message is meaningless to anyone except me and the intended recipient :). I really had fun in setting this problem :D.

ACM ICPC Jakarta 2012 - Problem H - Alien Abduction

During the interview with the champion team (+1 ironwood branch), Pi-Hsun (Peter) Shih said that his favorite problem is problem H (this problem). I should've asked why did he like it? is it because of the problem statement? or because he had fun in writing the solution :). Anyway, this problem is set by me and I would like to tell you how this problem was created / prepared.

Initially, this problem was set to be "easier", that a simple K-d Tree or Quadtree solution will work fine. However, since Problem D is already using K-d Tree for finding the nearest neighbors, to give good variations to the problemset, I rewrote this problem so that it is NOT solvable using (static) K-d Tree nor Quadtree (unless you are able to code "dynamic" K-d Tree / Quadtree in contest time :P).

This problem is solvable using Range Tree. I taught Range Tree during Pelatnas (training camp) 3 TOKI 2012 to 8 of Indonesian students to prepare them for IOI 2012. There are several other students from University of Indonesia were present during the training camp and those same students were participating in ICPC Jakarta 2012. I was surprised that they didn't get this problem accepted in contest time!

I think Range Tree is a rare problem in programming contest. I won't discuss it in detail here, since it is a classic algorithm in computational geometry, you can search for it to learn more. Perhaps it will be included in the next version of the Competitive Programming Book. Rare problems like this usually become the "decider problems" that set apart teams at the top.

Many (inexperienced) teams were submitting naive (not even clever) brute-force solutions O(N*Q). Of course they will get "No - Time Limit Exceeded" reply. Then, they tried optimizing on reading the input more efficiently, optimize the loop, etc, but the complexity is still the same O(N*Q). This problem can be a time-waster for inexperienced teams. As the problem setter, I feel sorry for them.

Here is the problem statement, you can try submit your solution below.

I'd like to talk about how this problem was prepared, to give you an idea what is it like to be a problem setter. It took me a lot of time to prepare, especially for the test data since I have to kill off simple/clever brute-force solutions. Moreover, I have to kill off solutions using (static) K-d Tree and Quadtree :)

For the test cases, I prepared 4 types of tests:

1. To kill off plain bruteforce solutions O(Q*N), a simple random positions and random alien abductions positions and energy will do. However, if we keep the people positions in sorted order, O(Q*N) solution can run pretty fast! So,
2. To kill off brute force solutions with sorted Xi and Yi coordinate, I created tests where the positions of the people have very close to each other in X coordinate but random in Y coordinate, and vice-versa. Thus bruteforce solutions that sort by X will still have to iterate many Y positions, and vice-versa. However, if we localized the coordinates, that is, by grouping all people in nearby coordinate (within 1000 distance), then you can prune a lot of people (given the energy and position of the alien ship), and thus the first two kinds of test case can run pretty fast! So,
3. To kill off nearby/localized spatial indexing solutions, I created test cases where all the people are in coordinate (0 <= Xi,Yi < 1000) and all the alien abductions operations are everywhere randomly with very large energy, but so that no abduction is happening. This will force the all local groups to be scanned every query because the energy is large enough to cover all the group in one axis or another (but not both). With these three kinds of tests, I am still concerned that K-d tree or Quadtree indexing will pass. So,
4. To kill off K-d Tree and Quadtree solutions, I set the positions of all people to (0 <= Xi,Yi < 10) initially. Then, I move (using the alien abduction operation) the person with identifier = 1 to the right 7000 times, and then move it 8000 times on the other (perpendicular) axis. Then, the next alien abduction operation will spread randomly the rest of the people all over the Earth. Then followed by a random alien abductions as in the first kind of testcase. So, if you were to index the INITIAL positions using (static) indexing data structure, and you don't rebalance your index tree during the translation, your index will be very skewed and unbalanced once they are translated and scattered to another part of Earth with clean index. This test case also kills off those who don't actually delete nodes from the K-d Tree / Quadtree (i.e, you flag the nodes as deleted), because the alien abductions will cover the initial positions often, and thus those "ghost nodes" will be revisited again and again if they are only flagged (not deleted).
5. If the contestants are cleverer than this, I will happily accept their solutions :)

There is one team I know (Azureus_HKU) using a clever brute-force that I didn't anticipate. They create a multimap for each x-coordinate, so for each x-coordinate they can know wheater there are people abducted in log(N), by binary searching the y-coordinate. But fortunately, the 3rd kind of testcase above also kills of this solution :). This clever brute-force algorithm can still run in O(1000*Q*log(N)) if the input is like this: all people are at coordinate between (0 <= Xi,Yi < 1000) and the alien abduction operations are at Xk = 5000, Yk = 0, Ek = 4000. What will happen is that each query, you need to scan/iterate all 1000 distinct X coordinate (and immediately find that the Y coordinate is not qualified). Thus it will need to iterate Q*1000*log(N) = 50000 * 1000 * 10 = TLE. It took 15+ seconds, while the Range Tree solution is around 5 seconds. BTW, the time limit for the problem is 10 seconds, which is quite generous :)

This is the input generator for problem H. You can try to test whether your bruteforce solution will pass the 10 second time limit. Remember to compile your C++ program WITHOUT using any optimizations.

So how does this Range Tree solution works? you asked. Well, we have to wait for our beloved chief of judge, Suhendry Effendy, to write a blog post about it. Please kindly remind him every now and then, because he often forgot to blog >:D.

MapReduce-Based Maximum-Flow Algorithm for Large Small-World Network Graph

Felix Halim, Roland H.C. Yap, Yongzheng Wu

[ ICDCS11 Paper ]

Abstract

Maximum-flow algorithms are used to find spam sites, build content voting system, discover communities, etc., on graphs from the Internet. Such graphs are now so large that they have outgrown conventional memory-resident algorithms. In this paper, we show how to effectively parallelize a max-flow algorithm based on the Ford-Fulkerson method on a cluster using the MapReduce framework. Our algorithm exploits the property that such graphs are small-world networks with low diameter and employs optimizations to improve the effectiveness of MapReduce and increase parallelism. We are able to compute max-flow on a subset of the a large social network graph with 411 million vertices and 31 billion edges using a cluster of 21 machines in reasonable time

Background and Motivation

Nowdays, the real-world graphs (such as WWW, Social Networks, etc.) have grown very large. For example, a Facebook graph with 700 million users where each user has 130 friends on average, requires a storage space of 700 * 10^6 * 130 * 4 bytes = 364 Gigabytes just to store the relationships alone. Even if we have a super computer with Terabytes of memory, it is unclear whether running the best maxflow algorithm on such large graph can be practical (the current best maxflow algorithm has a complexity of at least quadratic in respect of the number of vertices).

In this paper, we investigate the feasibility of computing maxflow on a very large small-world network (SWN) graph. One of the property of a SWN graph is that it has a very small (expected) diameter (the shortest path length between any two vertices in the graph is expected to be small). This allows us to develop variants of the Ford-Fulkerson method to compute maxflow effectively for SWN graphs. Since we are dealing with a type of graph which size is far larger than a single machine memory capacity, we took an appoach to distribute the graph into several machines in a cluster to be processed in parallel. Currently, MapReduce has become the facto standard to store, manage, and process very large datasets on a cluster of thousands of commodity machines. We designed an developed our maxflow variants to work on top of the MapReduce framework.

The Challenges and Approach

The classical maxflow algorithms were designed under assumption that the entire graph is small enough fit into main memory. Such algorithms are not directly applicable to run on distributed systems (such as MapReduce framework) since it require a global view of the entire graph. On the other hand, the existing distributed maxflow algorithm based on the Push-Relabel algorithm, while it can work in local manner, is too reliant on heuristics to push the flow. A wrong push can cause a very large number of MR rounds spent circling around the flow, thus is not suitable for MapReduce. However, in a system where performing one round is cheap (using Bulk-Synchronous Parallel model), Push-Relabel should perform much better.

We decided to develop maxflow variants based on the Ford-Fulkerson method. With assumption that the graphs being processed have small diameter, we transformed the naive (sequential) Ford-Fulkerson method into a highly parallelizable MR algorithm variants by finding augmenting paths incrementally, bi-directional search, and multiple excess paths. In the next subsections we illustrate the inner working of the naive Ford-Fulkerson method and the variants. Notice the number of MR rounds required for each variant (the lower the better). We combined these variants together to form an effective maxflow algorithm on MR framework which we called FF1_MR.

The Naive Ford-Fulkerson Method

The naive Ford-Fulkerson method works by repeatedly find an augmenting path in the current residual graph and augment it:

while true do
    P = find an augmenting path in the current residual graph Gf
    if (P does not exist) break
    Augment the flow f along the path P

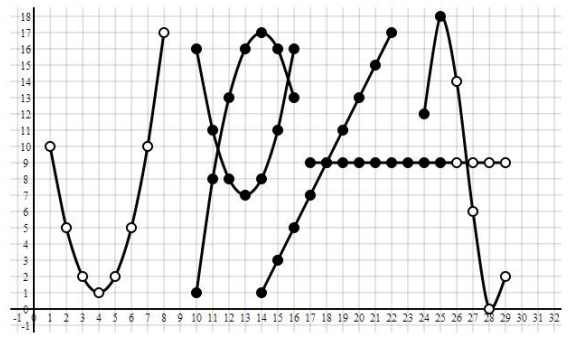
The Ford-Fulkerson method does not dictate how to find an augmenting path. The naive way to find it is to use Breadth-First Search (BFS). The complexity of this method is O(|f*| D) rounds, where |f*| is the maxflow value and D is the diameter of the graph. Note that in MR algorithms, we measure the complexity in terms of number of MR jobs (or rounds) performed. Below is an illustration on how the maxflow can be found using this way.

Round :

Finding Augmenting Paths Incrementally

An improvement from the previous method is to incrementally find the augmenting paths. That is, we don't re-start the BFS from scratch everytime an augmenting path is found. Instead, we continue the work from the previous round's result by updating parts of the graph and only destroy/remove the results that aren't fruitful.

The incremental finding of augmenting paths reduces the complexity to be far lower than O(|f*| D) rounds since an augmenting path may arrive continuously every subsequent rounds. We expect the complexity to be O(|f*|) rounds.

Round :

Bi-Directional Search

Bi-directional search is a two-way search: one originates from the source vertex s and the other is from the sink vertex t. This doubles the utilization of work per round, so that more work can be done each round. This also effectively halves the number of rounds required to complete the maxflow. We allow more than one augmenting path to be accepted per round. The expected complexity of this variant is O(|f*| / A) rounds, where A is the average number of augmenting paths accepted per round. Below is the illustration of the bi-directional search variant, improving the incremental updates variant.

Round :

Multiple Excess Paths

When an augmenting path is found and augmented, many vertices will lose its excess path if they are conflict with the augmenting path. To prevent vertices to lose all of its excess paths, we allow each vertex to store K excess paths so that even though large number of augmenting paths are augmented, many of the vertices will still be active and continue to give streams of new augmenting paths every round.

Round :

Among all variants described above, this multiple excess paths variant gives the most decrease in the number of rounds. The complexity of these variants altogether is O(|f*| / A) where A is the number of augmenting paths accepted per round. The value of A is very large such that the complexity becomes very close to O(D).

The experiment result above shows that the number of excess path stored in each vertex (K) have significant impact in computing maxflow of two random vertices s and t on a social network subgraph (FB1) with 21 million vertices and 112 million edges. The more the K the less the number of MR rounds required. On a very large value of K, the number of rounds becomes close to the diameter of the graph.

MapReduce Optimizations

MapReduce is a general purpose framework. It is not necessarily the best framework to process graph-based data. In this section we describe our MR optimizations to work around the limitations of MR in processing graph-based data. We implemented each optimization into a variant of our FF1_MR algorithm:

FF2_MR : Stateful Extension for MR

When there are a lot of augmenting paths found in one round, we must have a (single threaded) worker that decides which augmenting paths to be accepted and which are to be rejected. In FF1, this decision is made by one of the reducers that is responsible for vertex t. The larger the number of augmenting paths, the longer that reducer need to run. This can cause a convoy effect where the other reducers are already finish but the reducer which process vertex t lags behind.

This lead us to create an extension for MR, that is a dedicated worker outside MR which job is to process augmenting paths that are generated in each round by the reducers. This has advantages that the dedicated worker can start working as soon as it receives augmenting paths from the reducers. It doesn't need one extra step to send augmenting paths (as messages) to vertex t which wastes one MR round. This stateful extension solves the bottleneck of FF1_MR.

The improvement it brings is significant. FF2_MR improvement is up to 3.41 times faster for FB4 and 1.85 times faster for FB1.

FF3_MR : Schimmy method

Schimmy method is an MR design pattern for processing graph-based data. The improvement is more apparent for larger graph FB4 (1.74 times) and lesser for smaller graph FB1 (1.25 times).

FF4_MR : Avoid Object Instantiations

This is a common optimizations. The improvement is around 1.16 - 1.41 times.

FF5_MR : Storage Space vs. number of rounds and communication costs

The last but not least optimization is to avoid sending messages (as intermediate records) each round by sacrificing some storage space (used as flags). We can also sacrifice storage space by storing maximum number of excess paths (set K = 5000) to reduce the number of rounds. We avoid sending delta updates as messages (as intermediate records) if we can re-compute the delta in the reducers.

We found a high correlation between the number of shuffled bytes and the runtime and in this variant, we try to minimize the number of shuffled bytes as much as possible. The reduce shuffle bytes depends on the number and the size of the intermediate records. The experiment above shows the number of bytes shuffled for each variant (from FF1 to FF5).

FF1 is the worst since it sends all the augmenting paths found in the current round to vertex t as messages. Therefore there from round #4 to #8 the reduce shuffle bytes is high. FF2 uses the external worker to immediately process the augmenting paths, therefore the reduce shuffle bytes for round #4 to #8 is small, however, it grows afterwards since every active vertices always re-send its excess path to its neighbors. FF3 avoid the master graph to be shuffled, so it is a consistent improvement over FF2. FF4 doesn't reduce the shuffled bytes, hence not shown here. FF5 sets the K to maximum and prevent redundant messages (by recomputing or by flag). FF5 manages to keep the shuffled bytes small and it is the best of our MR variants.

Scalability

We tested our FF5_MR variant for very large flow value on a very large social network subgraph (FB6) with 411 million vertices and 31 billion edges. To create a very large flow, we combine w = 128 random vertices and create a super source vertex s, and similarly with the super sink t. The flow between the super source and the super sink can be up to 128 * 5000 = 640,000.

The experiment shows that even for such large maxflow values, the number of rounds required to compute the maxflow stay small (around 7 to 8 rounds). This suggest that the approaches that we've put in FF1_MR are effective in minimizing the number of rounds. The runtime increases linearly while the maxflow value increases exponentially. This shows the scalability of our FF_MR in handling a very large maxflow value.

Another scalability test is in terms of graph size and number of machines (from 5 to 20 machines). We plot the runtime and number of rounds required to compute maxflow on several subgraphs (FB1 to FB6). We also created the super source and the super sink for w = 128 (the vertices are randomly chosen in the subgraph). We also plot the best case scenario of running a single Breadth-First Search on each subgraph.

The experiment shows that our best variant, FF5_MR, is only a constant factor slower than a BFS_MR! The maxflow value is writen under the subgraph name (FB1 to FB6). If we see the graph in terms of number of edges processed per second:

The experiment shows that the larger the graph, the higher the number edges processed per second. This may mean several things: the larger the graph, the smaller its diameter and the more robust the graph (that is, despite the large number of deletion of edges in the residual graph, the graph still maintain small diameter).

Conclusion and Future Work

We developed what we believe to be the first effective and practical max-flow algorithms for MapReduce. While the best sequential max-flow algorithms have around quadratic runtime complexity, we show it is still possible to compute max-flow efficiently and effectively on very large real-world graphs with billions of edges. We achieve this by designing FF_MR algorithms that exploit the small diameter property of such real-world graphs while providing large amounts of parallelism. We also present novel MR optimizations that significantly improve the initial design which aim to minimize the number of rounds, the number of intermediate records, the size of the biggest record. Our optimizations also exploit tradeoffs between space needed for the data and number of rounds. Our preliminary experiments show a promising and scalable algorithm to compute max-flow for very large real-world social network sub-graphs.

We still see several rooms for improvement such as optimizing the last few rounds as well as giving an approximation of a maxflow value to get faster runtime. We also see the need to benchmark with custom build Graph framework which optimizes the memory management in the case where the entire graph fit to the total memory capacity of a cluster of machines. A comparison with the Push-Relabel algorithm implemented on a Bulk-Synchronous Parallel would be a good direction as well.

Facebook Hacker Cup 2011 Qualification Round

Aside from the poorly organized contest, I will discuss my solutions for the 3 problems presented. Apparently I didn't save the problem descriptions and the site is down at the moment. However, a quick search on "double squares peg games studious student" will give you the problem descriptions and perhaps other solutions in other languages.

Problem 1 - Double Squares

This problem can be solved in linear time O(sqrt(2^31)) = O(46341) per test case. The idea is to find two pairs (L,R) that satisfy L*L + R*R == X. We begin from L = 0 and R = 46341 and start scanning. It can be proven that if (L*L + R*R > X) then the next "satisfying pair" (L,R) will be on (L,R-1), similarly on the two other cases.

#include <stdio.h>

int main(){
    int N,X,res;
    scanf("%d",&N);
    while (N--){
        scanf("%d",&X);
        long long L=res=0, R=46341;     // R = sqrt(2^31)
        while (L<=R){
            long long Y = L*L + R*R;
            if (Y > X) R--;
            else if (Y < X) L++;
            else res++, L++;
        }
        printf("%d\n",res);
    }
}

Problem 2 - Peg Game

Dynamic Programmers veteran will immidiately see the solution :). We can first set the last row probability to zero except the goal's column which have probability one. Then we can start filling out the probabilites for the second to last row and so on up to the first row. We only need to calculate probability for empty cells '.'. If the cell has two possible branches, the probability is taken 0.5 and 0.5 from each branch. Otherwise, the full probability of the only branch is copied (as well as for the fall through case).

#include <stdio.h>
#include <string.h>

#define REP(i,n) for (int i=0,_n=n; i<_n; i++)

double p[111][222];
char m[111][222];
int N,R,C,K,M,r,c;

int main(){
    scanf("%d",&N);
    while (N--){
        scanf("%d %d %d %d",&R,&C,&K,&M);
        memset(m,'.',sizeof(m));                 // creates empty board
        REP(i,R){                                    
            if (i%2==0){
                REP(j,C) m[i][2*j] = 'x';        // pegs for the odd rows
            } else {
                REP(j,C-1) m[i][2*j+1] = 'x';    // pegs for the even rows
                m[i][0] = m[i][2*C-2] = ' ';     // wall on the left and right
            }
        }

        REP(i,M) scanf("%d %d",&r,&c), m[r][2*c + r%2] = '.';    // mark missing pegs

        REP(i,C) p[R-1][2*i+1] = 0.0;    // clear last row probability
        p[R-1][2*K+1] = 1.0;             // set the goal probability = 1.0

        for (int i=R-2; i>=0; i--)                 // do dynamic programming from bottom to top
            REP(j,2*C-1) if (m[i][j]=='.'){        // only calculate probability for empty cells
                if (m[i+1][j]=='x'){
                    if (m[i+1][j-1]==' ') p[i][j] = p[i+1][j+1];         // only consider right
                    else if (m[i+1][j+1]==' ') p[i][j] = p[i+1][j-1];    // only consider left
                    else p[i][j] = (p[i+1][j+1] + p[i+1][j-1]) / 2.0;    // consider both
                } else if (m[i+1][j]=='.'){
                    p[i][j] = p[i+1][j];           // fall through
                }
            }

        int col = 0; double maxp = -1;
        REP(j,C-1) if (p[0][j*2+1] > maxp)      // loop through the first row
            maxp = p[0][j*2+1], col = j;        // and keep track the best probability
        printf("%d %.6lf\n",col,maxp);
    }
}

Problem 3 - Studious Student

Again, Dynamic Programming is the way. The DP state is dp[mask] = the least lexicographic string using the words in the mask. The answer is dp[(1<<M)-1], that is the least lexicographic string using all the words.

#include <stdio.h>
#include <string>
#include <vector>

using namespace std;

#define REP(i,n) for (int i=0,_n=n; i<_n; i++)

string memo[1<<10];
vector<string> vs;
char s[1000];
int N,M;

string rec(int mask){
    if (mask == (1<<M)-1) return "";
    string &ret = memo[mask];
    if (ret != "{") return ret;
    REP(i,M) if (!(mask & (1<<i)))
        ret = min(ret, vs[i] + rec(mask|(1<<i)));
    return ret;
}

int main(){
    scanf("%d",&N);
    while (N--){
        scanf("%d",&M);
        vs.clear();
        REP(i,M) scanf("%s",s), vs.push_back(s);
        REP(i,1<<M) memo[i] = "{";
        puts(rec(0).c_str());
    }
}

Update: Eko Wibowo mentioned that a simple sort is enough, using the following comparison function:

bool cmp(const string &a, const string &b){
    return (a+b) < (b+a);
}

Update: Suhendry mentioned that this problem is similar to this problem. The first two problems are also not original according to some TopCoders (see the TopCoder forum).